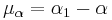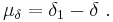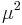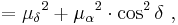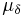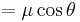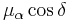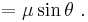Proper motion

The proper motion of a star is its angular change in position over time as seen from the center of mass of the solar system.[1] It is measured in seconds of arc per year, arcsec/yr, where 3600 arcseconds equal one degree.[2] This contrasts with radial velocity, which is the time rate of change in distance toward or away from the viewer, usually measured by Doppler shift of received radiation. The proper motion is not entirely "proper" (that is, intrinsic to the star) because it includes a component due to the motion of the solar system itself.[3] Due to the finite speed of light, the true velocities of distant stars are not observable, the observed proper motion reflects the motion of a star at the time the light was emitted.

Contents

Introduction

Over the course of centuries, stars appear to maintain nearly fixed positions with respect to each other, so that they form the same constellations over historical time. Ursa Major, for example, looks nearly the same now as it did hundreds of years ago. However, precise long-term observations show that the constellations change shape, albeit very slowly, and that each star has an independent motion.

This motion is caused by the true movement of the stars relative to the Sun and solar system through space. The Sun travels in a nearly circular orbit (the solar circle) about the center of the Milky Way at a speed of about 220 km/s at a radius of 8 ± 0.65 kpc from the center,[4][5] which can be taken as the rate of rotation of the Milky Way itself at this radius.[6][7]

The proper motion is measured by two quantities: the position angle and the proper motion itself. The first quantity indicates the direction of the proper motion on the celestial sphere (with 0 degrees meaning the motion is due north, 90 degrees meaning the motion is due east, and so on), and the second quantity gives the motion's magnitude, in seconds of arc per year.

Proper motion may also be given by the angular changes per year in the right ascension (μα) and declination (μδ). On the celestial sphere, positions are located by latitude and longitude. The coordinate δ corresponds to latitude. The coordinate α corresponds to longitude measured from the vernal equinox V, the point on the sky where the Sun crosses the celestial equator on near March 21.[3]

The components of proper motion by convention are arrived at as follows. Suppose in a year an object moves from coordinates (α, δ) to coordinates (α1, δ1), with angles measured in seconds of arc. Then the changes of angle in seconds of arc per year are:[8]

\ \mu_{\alpha} = \alpha_1 - \alpha \
\ \mu_{\delta}=\delta_1-\delta \ .

The magnitude of the proper motion μ is given by vector addition of its components:[9][10]

\ \mu^2 ={\mu_\delta}^2 %2B {\mu_\alpha}^2 \cdot \cos^2 \delta \ ,

where δ is the declination. The factor in cos δ accounts for the fact that the radius from the axis of the sphere to its surface varies as cos δ, becoming, for example, zero at the pole. Thus, the component of velocity parallel to the equator corresponding to a given angular change in α is smaller the further north the object's location. The change μα , which must be multiplied by cos δ to become a component of the proper motion, is sometimes called the "proper motion in right ascension", and μδ the "proper motion in declination".[11]

The position angle θ is related to these components by:[12][13]

\ \mu_\delta =\mu \cos \theta\
\ \mu_\alpha \cos \delta =\mu \sin \theta\ .

Barnard's star has the largest proper motion of all stars, moving at 10.3 seconds of arc per year. Large proper motion is usually a strong indication that a star is relatively close to the Sun. This is indeed the case for Barnard's Star which, at a distance of about 6 light-years, is, after the Sun and the Alpha Centauri system, the nearest known star to Earth (yet, being a red dwarf, too faint to see without a telescope or powerful binoculars, with an apparent magnitude of 9.54).

In 1992, Rho Aquilae became the first star to have its name invalidated by moving to a neighbouring constellation - it is now a star of the constellation Delphinus.[14] This will next happen to Gamma Caeli, which is due to become a star of the constellation Columba in the year 2400.[15]

A proper motion of 1 arcsec per year at a distance of 1 light-year corresponds to a relative transverse speed of 1.45 km/s. For Barnard's star this works out to 90 km/s; including the radial velocity of 111 km/s (which is at right angles to the transverse velocity) gives a true motion of 142 km/s. True or absolute motion is more difficult to measure than the proper motion, as the true transverse velocity involves the product of the proper motion times the distance; that is, true velocity measurements depend on distance measurements, which are difficult in general. Currently, the nearby star with the largest true velocity (relative to the Sun) is Wolf 424 which moves at 555 km/s (or 1/540 of the speed of light).

Usefulness in astronomy

Stars with large proper motions tend to be nearby; most stars are far enough away that their proper motions are very small, on the order of a few thousandths of an arcsecond per year. It is possible to construct nearly complete samples of high proper motion stars by comparing photographic sky survey images taken many years apart. The Palomar Sky Survey is one source of such images. In the past, searches for high proper motion objects were undertaken using blink comparators to examine the images by eye, but modern efforts use techniques such as image differencing to automatically search through digitized image data. Because the selection biases of the resulting high proper motion samples are well-understood and well-quantified, it is possible to use them to construct an unbiased census of the nearby stellar population — how many stars exist of each true brightness, for example. Studies of this kind show that the local population of stars consists largely of intrinsically faint, inconspicuous stars such as red dwarfs.

Measurement of the proper motions of a large sample of stars in a distant stellar system, like a globular cluster, can be used to compute the cluster's total mass via the Leonard-Merritt mass estimator. Coupled with measurements of the stars' radial velocities, proper motions can be used to compute the distance to the cluster.

Stellar proper motions have been used to infer the presence of a super-massive black hole at the center of the Milky Way.[16] This black hole is suspected to be Sgr A*, with a mass of 2.6 × 106 M☉, where M☉ is a solar mass.

Proper motions of the galaxies in the Local Group are discussed in detail in Röser.[17] In 2005, the first measurement was made of the proper motion of the Triangulum Galaxy M-33, the third largest and only ordinary spiral galaxy in the Local Group, located 860 ± 28 kpcs beyond the Milky Way.[18] Although the Andromeda Galaxy is known to move, and an Andromeda-Milky Way collision is predicted in about 5 – 10 billion years, the proper motion of the Andromeda galaxy, about 786 kpc distant, is still an uncertain matter, with an upper bound on its transverse velocity of ≈ 100 km/s.[7][19][20] Proper motion of the NGC 4258 (M106) galaxy in the M106 group of galaxies was used in 1999 to find an accurate distance to this object.[21] Measurements were made of the radial motion of objects in that galaxy moving directly toward and away from us, and assuming this same motion to apply to objects with only a proper motion, the observed proper motion predicts a distance to the galaxy of 7.2 ± 0.5 Mpc.[22]

History

Proper motion was suspected by early astronomers (according to Macrobius, AD 400) but proof was provided in 1718 by Edmund Halley, who noticed that Sirius, Arcturus and Aldebaran were over half a degree away from the positions charted by the ancient Greek astronomer Hipparchus roughly 1850 years earlier.[23]

The term "proper motion" derives from the historical use of "proper" to mean "belonging to" (cf, propre in French), so there is no such thing as "improper motion" in astronomy.[1]

Stars with high proper motion

The following are the stars with highest proper motion from the Hipparcos catalog.[24](see List of stars in the Hipparcos Catalogue) It does not include stars such as Teegarden's star which are too faint for that catalog. A more complete list of stellar objects can be made by doing a Criteria query at http://simbad.u-strasbg.fr/simbad/ .

Highest proper motion stars[25]
# Star Proper motion Radial
velocity
(km/s)		 Parallax
(mas)
μα · cos δ
(mas/yr)		 μδ
(mas/yr)
1 Barnard's star -798.71 10337.77 -106.8 549.30
2 Kapteyn's star 6500.34 -5723.17 +245.5 255.12
3 Groombridge 1830 4003.69 -5814.64 -98.0 109.22
4 Lacaille 9352 6766.63 1327.99 +9.7 303.89
5 Gliese 1 (CD -37 15492) (GJ 1) 5633.95 -2336.69 +23.6 229.32
6 HIP 67593 2282.15 5369.33 — 76.20
7 61 Cygni A & B 4133.05 3201.78 -64.3 287.18
8 Lalande 21185 -580.46 -4769.95 -85.0 392.52
9 Epsilon Indi 3961.41 -2538.33 -40.4 275.79

Software

There are a number of software products that allow a person to view the proper motion of stars over differing time scales. Two free ones are:

See also

References

  1. ^ a b Theo Koupelis, Karl F. Kuhn (2007). In Quest of the Universe. Jones & Bartlett Publishers. p. 369. ISBN 0763743879. http://books.google.com/?id=6rTttN4ZdyoC&pg=PA369. 
  2. ^ Simon F. Green, Mark H. Jones (2004). An Introduction to the Sun and Stars. Cambridge University Press. p. 87. ISBN 0521546222. http://books.google.com/?id=lb5owLGIQGsC&pg=PA87. 
  3. ^ a b D. Scott Birney, Guillermo Gonzalez, David Oesper (2007). Observational astronomy. Cambridge University Press. p. 73. ISBN 0521853702. http://books.google.com/?id=cc9L8QWcZWsC&pg=RA1-PA73. 
  4. ^ Horace A. Smith (2004). RR Lyrae Stars. Cambridge University Press. p. 79. ISBN 0521548179. http://books.google.com/?id=dMv_r82moCQC&pg=PA80&dq=Galactocentric+%22solar+circle%22. 
  5. ^ M Reid, A Brunthaler, Xu Ye et al. (2008). "Mapping the Milky Way and the Local Group". In F. Combes, Keiichi Wada. Mapping the Galaxy and Nearby Galaxies. Springer. ISBN 0387727671. http://books.google.com/?id=bP9hZqoIfhMC&pg=PA24&dq=rotation+%22proper+motion%22+galaxy+OR+galactic. 
  6. ^ Y Sofu & V Rubin (2001). "Rotation Curves of Spiral Galaxies". Ann. Rev. Astron. Astrophys. 39: 137–174. arXiv:astro-ph/0010594. Bibcode 2001ARA&A..39..137S. doi:10.1146/annurev.astro.39.1.137. 
  7. ^ a b Abraham Loeb, Mark J. Reid, Andreas Brunthaler, Heino Falcke (2005). "Constraints on the proper motion of the Andromeda galaxy based on the survival of its satellite M33". The Astrophysical Journal 633: 894–898. arXiv:astro-ph/0506609. Bibcode 2005ApJ...633..894L. doi:10.1086/491644. http://www.mpifr-bonn.mpg.de/staff/abrunthaler/pub/loeb.pdf. 
  8. ^ William Marshall Smart, Robin Michael Green (1977). Textbook on Spherical Astronomy. Cambridge University Press. p. 252. ISBN 0521291801. http://books.google.com/?id=W0f2vc2EePUC&pg=PA252. 
  9. ^ Charles Leander Doolittle (1890). A Treatise on Practical Astronomy, as Applied to Geodesy and Navigation. Wiley. p. 583. http://books.google.com/?id=3HoAAAAAMAAJ&pg=RA1-PA583. 
  10. ^ Majewski, Steven R. (2006). "Stellar Motions". University of Virginia. http://www.astro.virginia.edu/class/majewski/astr551/lectures/VELOCITIES/velocities.html. Retrieved 2007-05-14. 
  11. ^ Simon Newcomb (1904). The Stars: A study of the Universe. Putnam. pp. 287–288. http://books.google.com/?id=OG1AAAAAIAAJ&pg=PA287. 
  12. ^ D. Scott Birney, Guillermo Gonzalez, David Oesper (2007). op. cit.. p. 75. ISBN 9780521853705. http://books.google.com/?id=cc9L8QWcZWsC&pg=RA1-PA9&dq=celestial+sphere+%22right+ascension%22. 
  13. ^ See Majewski, Steven R. (2006). "Stellar motions: parallax, proper motion, radial velocity and space velocity". University of Virginia. http://www.astro.virginia.edu/class/majewski/astr551/lectures/VELOCITIES/velocities.html. Retrieved 2008-12-31. 
  14. ^ "Book-Review - Sky Catalogue 2000.0 - V.1 - Stars to Magnitude 8.0 ED.2". 1992. http://articles.adsabs.harvard.edu//full/1992JRASC..86..221H/0000222.000.html. Retrieved 2008-05-16. 
  15. ^ "Hamilton Amateur Astronomers". 1996. http://amateurastronomy.org/EH/Jun96.txt. Retrieved 2008-05-16. 
  16. ^ AM Ghez et al. (2003). "The First Measurement of Spectral Lines in a Short-Period Star Bound to the Galaxy's Central Black Hole: A Paradox of Youth". Astrophysical Journal 586: L127–L131. arXiv:astro-ph/0302299. Bibcode 2003ApJ...586L.127G. doi:10.1086/374804. 
  17. ^ Andreas Brunthaler (2005). "M33 – Distance and Motion". In Siegfried Röser. Reviews in Modern Astronomy: From Cosmological Structures to the Milky Way. Wiley. pp. 179–194. ISBN 3527406085. http://books.google.com/?id=P3FAxGsJ_B8C&pg=PA189&dq=M33+%22proper+motion%22. 
  18. ^ A. Brunthaler, M.J. Reid, H. Falcke, L.J. Greenhill, C. Henkel (2005). "The Geometric Distance and Proper Motion of the Triangulum Galaxy (M33)". Science 307 (5714): 1440–1443. arXiv:astro-ph/0503058. Bibcode 2005Sci...307.1440B. doi:10.1126/science.1108342. PMID 15746420. 
  19. ^ Roeland P. van der Marel (2008). "M31 Transverse Velocity and Local Group Mass from Satellite Kinematics". The Astrophysical Journal 678: 187–199. Bibcode 2008ApJ...678..187V. doi:10.1086/533430?cookieSet=1&journalCode=apj. 
  20. ^ Manuel Metz, Pavel Kroupa, Helmut Jerjen (2007). "The spatial distribution of the Milky Way and Andromeda satellite galaxies". Mon. Not. Roy. Astron. Soc. 374: 1125–1145. arXiv:astro-ph/0610933. Bibcode 2007MNRAS.374.1125M. doi:10.1111/j.1365-2966.2006.11228.x. 
  21. ^ Steven Weinberg (2008). Cosmology. Oxford University Press. p. 17. ISBN 0198526822. http://books.google.com/?id=48C-ym2EmZkC&pg=PA17&dq=M33+%22proper+motion%22+date:2007-2010. 
  22. ^ J. R. Herrnstein et al. (1999). "A geometric distance to the galaxy NGC4258 from orbital motions in a nuclear gas disk". Nature 400 (6744): 539–541. arXiv:astro-ph/9907013. Bibcode 1999Natur.400..539H. doi:10.1038/22972. http://www.nature.com/nature/journal/v400/n6744/abs/400539a0.html. 
  23. ^ Otto Neugebauer (1975). A History of Ancient Mathematical Astronomy. Birkhäuser. p. 1084. ISBN 354006995X. http://books.google.com/?id=vO5FCVIxz2YC&pg=PA1085&dq=proper+motion+angle. 
  24. ^ Staff (September 15, 2003). "The 150 Stars in the Hipparcos Catalogue with Largest Proper Motion". ESA. http://www.rssd.esa.int/SA-general/Projects/Hipparcos/table362.html. Retrieved 2007-07-21. 
  25. ^ "SIMBAD". Centre de Données astronomiques de Strasbourg. http://simbad.u-strasbg.fr/simbad/. Retrieved 2007-07-21. 

External links

Evolution
Protostars
Luminosity class
Spectral classification
Remnants
Failed and
theoretical stars
Nucleosynthesis
Structure
Properties
Star systems
Earth-centric
observation of
Lists
Related articles
Star portal